It’s scary how much people believe in science.
Stephen Wolfram
Immanuel Kant, perhaps the most important philosopher of modernity, hated determinism. How could man retain what made him most humane in the face of the unfolding clockwork of the universe? (Wo)man, after all, is (wo)man only because she chooses, and choosing what is right allows her to act morally, allows her to realize her innermost humaneness.
If it were possible to know the position and velocity of every particle in the universe, then we could predict with utter precision the future of those particles and, therefore, the future of the universe.
Isaac Newton
Since the days of Newton, professional thinkers and non-professional thinkers alike have been struggling with the idea of determinism. For us, caught up in the heat of the moment, trapped in the light cone of relativity that limits the boundaries of what we can ever know anything about, our heads filled with an inference machine trying to predict the future based on sparse information flowing in from the outside in real time, determinism manifestly does not agree with our day-to-day experience.
I have noticed even people who claim everything is predestined look before they cross the road.
Stephen Hawking
The implications of determinism are usually caricatured as sucking all spontaneity and choice out of life. Determinism is billiard balls smashing into each other. Determinism is stale, precise like a clock ticking.
Free will, on the other hand, is fuzzy, exciting, dramatic. Free will, like a femme fatale in a film noir, is so appealingly erotic because it is so unpredictable.
In my article on Romanticism and the Divided Brain, I explored how philosophers and artists of the romantic era represented life as an unreliable, uncontrollable torrent, alive, and unknowable.
To keep holding onto this perspective on the world, romantic thinkers felt the dire need to somehow get rid of determinism, the intellectual straight-jacket that sucked out all the fun and glory out of existence: determinism implied that you could know everything, and knowing everything would be horribly boring.
The assumption of an absolute determinism is the essential foundation of every scientific inquiry.
– Max Planck
Yet at the same time, our scientific modes of inquiry into reality suggest that the assumption of determinism is absolutely necessary if we want to find out anything objective about the world. To balance these two positions, modern man walks around with a mild sense of cognitive dissonance in his head, arising from the friction between these two seemingly irreconcilable positions.
But I think that this does not have to be inadvertently so, and that science actually provides a perspective that allows us to square them, to accept that determinism is technically correct, but to also see in which sense it doesn’t really matter. Because a great many things are far too complex to know in advance, and life, even if we model it as well as we can, will always find a way to elude our grasp.
Fifty years ago Kurt Gödel… proved that the world of pure mathematics is inexhaustible.
Freeman Dyson
Gödel’s theorem was the thorn in the flesh of modern mathematics, bringing Hilbert’s ambitious Hilbertprogramm, a project that was to solve the foundational crisis of mathematics, to a grinding halt.
In the language of Turing machines, Gödel’s theorem was cast in a more intuitive way as the halting problem: it is the problem of determining froma description of a Turing machine and an input whether the program will ever come to a halt or continue to run forever.
Turing showed that a general algorithm to determine when all programs would stop logically could not exist, and that there would always exist programs that you would need to run up until the very end to figure out when or if they would stop.
This halting problem might seem to be a very specific problem, but it is important to emphasize that all computation can be formulated in terms of universal Turing machines, and that computation relates to more than just what we think of a computer doing in everyday life.
Stephen Wolfram, the founder of Wolfram Alpha (I’ll leave aside the controversies surrounding him here), thinks of all of reality as being constituted by simple computational processes, and that the halting problem hints at more fundamental questions revolving what he calls computational irreducibility.
In a similar sense to Turing’s halting problem, the theory of computational irreducibility it claims that not all complex computations allow for a simpler, reduced reformulation. According to Wolfram MathWorld, “ while many computations admit shortcuts that allow them to be performed more rapidly, others cannot be sped up. Computations that cannot be sped up by means of any shortcut are called computationally irreducible. The principle of computational irreducibility says that the only way to determine the answer to a computationally irreducible question is to perform, or simulate, the computation.”
“The good news is that we will never be able to predict everything.”
Stephen Wolfram
Science is about reduction. When we build models of the world, we try to discover simpler descrptions behind seemingly disparate phenomena and reduce them to the common denominator of an explanation. Take the example of Darwinian evolution: the incredible richness of life forms was discovered by Darwin to follow from the simplicity of mutation and selection.
But sometimes knowing the explanation behind a phenomenon only gets us so far.

Chaos theory was a surprisingly long time in the making, considering it tends to be, in the shape of pangs and arrows of outrageous weather, a constant companion in our everyday lives. But to this day, first-semester university students of the natural sciences are still mostly concerned with the peaceful harmony of the harmonic oscillator, or with the neat differential equations of the planetary orbits, allowing for predictions thousands of years into the future.
Only in the smaller and darker chambers of later semesters, the dirty secret of chaos theory is slowly admitted to: even if we have a description of a system, we might still not really know how the system will behave precisely, and where it will end up in the long run.

The Lorenz system is a famous and simple example of such a system. Originally discovered by Edvard Lorenz in 1963 (he was trying to find better models of the weather), it quickly became a favorite example for the strange properties of chaotic systems.
It is a 3D-system, which means it you can nicely draw it (see pictures below), and it traces out a curve in this three-dimensional space. The current position of the system will determine where it will end up in the next step, and if you don’t add any random noise at every time step, the system is fully deterministic.
But while it is deterministic, it is still in a sense impossible to predict.
Here is a short Python snippet that simulates a Lorenz system with initial state state0 for 4000 time steps, plots the curve and prints the final state:
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from mpl_toolkits.mplot3d import Axes3D#model parameters
rho = 28.0
sigma = 10.0
beta = 8.0 / 3.0
def f(state, t):
x, y, z = state # Unpack the state vector
return sigma * (y - x), x * (rho - z) - y, x * y - beta * z # Derivatives
state0 = [1.0, 1.0, 1.0] #initial state
t = np.arange(0.0, 40.0, 0.01) # number of time steps (here 4000)
states = odeint(f, state0, t)
fig = plt.figure()
ax = fig.gca(projection="3d")
ax.plot(states[:, 0], states[:, 1], states[:, 2])
plt.draw()
plt.show()
print(states[-1,:]) #print the final state
The peculiar property of chaotic system is that points that are very close to each other at one point in time quickly end up in very different places in the future. In more technical terms, the chaoticity of a system is described by the highest Lyapunov exponent of the system, which you can imagine as the speed with which a tiny (epsilon) environment around a point disperses through time.
Take, for example, two initial states that are extremely close to each other, and follow them along the system for 4000 time points:
Input state = [1.0, 1.0, 1.0]
Final state = [-1.96, -3.67, 9.19]Input state = [1.0001, 1.0001, 1.0001]
Final state =[ 4.23, 0.64, 27.42]
Both states end up in a completely different place in 3D-space. This is similar to what’s known as the butterfly effect: the wing of a butterfly can add a minute distortion to the initial state of a system such as the world. But the fact that the world is chaotic means that this minor distortion can blow up immensely, and the point you end up after waiting long enough will be completely different (e.g. life after the tornado caused by the butterfly hit your town and carried away your cows).
It turns out that an eerie type of chaos can lurk just behind a facade of order — and yet, deep inside the chaos lurks an even eerier type of order.
– Douglas Hofstadter
Nevertheless it’s interesting to observe that both chaotic trajectories look very similar while behaving in a different sense so unpredictable:
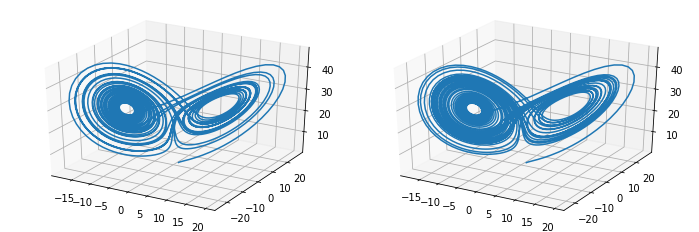
The great thing about chaotic systems is therefore that you can have a neat kind of order within them, but that knowing about this order only tells you about how the system will behave to a certain extent.
This brings us back to computational irreducibility, because that you can look at the Lorenz equations, paired with a set of initial condition, but you won’t be able to figure out where the system is on the attractor after 4000 time steps.
The only way to figure it out is to take follow the system one step at a time and see where the ride takes you.
It has to be noted that computational time does not have to equate physical time, and that computations are substrate-independent (more on how you can implement computation in my articles on Turing machines and the brain as a quantum computer). But the point still remains that the computation cannot be reduced to a simpler form, and if we think of reality as being constituted by computation, it really has to run through from start to finish if you want to know with any kind of certainty what the future brings.
It’s scary how much people believe in science.
Stephen Wolfram
Science is about reducing complex phenomena to simpler structures. But the study of complexity and chaos shows that a great many things can be practically impossible to reduce. This is true for so many system that the scientific question should rather be “which are the few systems that we can reduce enough to allow for reliable long-term predictions”.
This shouldn’t take away from us believing in the power of science, but rather communicate a more realistic picture of what science can in principle achieve and what it cannot achieve.
There is this idea that you would need to have the whole universe in order to simulate the universe, and the chaotic nature of many phenomena in reality show that from the inside it’s absolutely impossible to figure out the details of the route that it will take. Thus life, from the epistemological perspective of us that are caught up within it, remains a mystery unfolding. We that try to know it can never know it fully.
I think there is some meaning to be derived from the fact that reality is so irreducibly unknowable. Maybe it’s just a remnant from an over-romantization of reality, but to my mind, this makes all of this much more exciting: and maybe it can really be a consolation to all those similarily romantically inclined minds that determinism, as harsh as it sounds, doesn’t have to take away from the fun of it all.
About the Author
Manuel Brenner studied Physics at the University of Heidelberg and is now pursuing his PhD in Theoretical Neuroscience at the Central Institute for Mental Health in Mannheim at the intersection between AI, Neuroscience and Mental Health. He is head of Content Creation for ACIT, for which he hosts the ACIT Science Podcast. He is interested in music, photography, chess, meditation, cooking, and many other things. Connect with him on LinkedIn at https://www.linkedin.com/in/manuel-brenner-772261191/