“When one understands the causes, all vanished images can easily be found again in the brain through the impression of the cause. This is the true art of memory…” Rene Descartes, Cogitationes privatae.
Close your eyes (bad opening phrase when you’re trying to convince people to read your article) and imagine a face.
Now imagine a cat. A dog, house, car, sink, a bottle of beer, table, tree.
It’s all there in your head, easily conjured up in front of your inner eye, inner ear, within your inner world. But have you ever wondered what happens when you make up the image of something never before seen and never before heard?
We all have the ability to think up novel things that don’t exist. We shape visions of the future and suddenly experience ourselves in distant lands after seeing an ad in the tram.
And when we go to bed at night, with our eyes closed, shut off from all the fuzz of the world and from all sensory input, we dream up new worlds populated with people eerily similar to the ones we know from waking life.

What we can learn from this
Our ability to imagine so powerfully is a skill that neuroscientists and AI researchers alike are realizing is an important aspect of our intelligence. Modeling it, therefore, could be a crucial extension to our toolkit when building human-like intelligence.
But can we teach machines how to dream? Is this not something uniquely human, so very different from the precision and mechanical determinism of computers?
The answer is yes. Take a look at this merry assortment of people:




You can look at them and get a sense of how their lives might be. Where did they grow up? What high school did they go to? What are their personalities like? Are they rather serious fellows, or is that the trace of a cheeky smile?
They are people like you would imagine people to be. Perhaps like they would appear in your dreams.
The thing is that all four of them do not exist. They are a complete fabrication that I made my computer generate five minutes ago. That a computer dreamed up just like you would have dreamt them up.
How is this possible?
Different Shades of Randomness
Let’s take a couple of steps back.
Pictures are composed of hundreds of thousands of pixels, where each pixel contains individual color information (encoded with RGB, for example). If you randomly generate a picture (with every pixel is generated independently of all the others), it looks something like this:

If you generated a picture this way every second until a face showed up, you wouldn’t have gotten closer to your goal in a couple of billion years, and would still be generating pictures when the sun exploded in your face.
Most random pictures are not pictures of faces, and random pictures of faces are very much not random.
Latent Structure
There is a latent structure behind every face. Within the confines of this latent structure, there is some degree of flexibility, but it is much more constrained than not constrained.
Humans are quite good at understanding latent structure. We don’t think of faces in terms of pixels: we think of features like mouths and noses and ears and the distances (or lack thereof) between eyebrows, and we build an abstract representation in our mind of what a face is (much more in this on my article on The Geometry of Thought) that allows us to easily imagine a face, be it in our mind’s eye or by drawing it.
Finding latent structure in the world, in general, is not only immensely important for navigating and communicating within in it, and therefore for our survival, but the search for latent structure is in a sense the cornerstone of all scientific practice, and, arguably, intelligence (as I also went into more detail in my article on Why Intelligence Might be Simpler Than We Think).
Data, as we gather it from the external world, is generated by processes that are usually hidden from our view. Building a model of the world means searching for these hidden processes that generate the data we observe.
The laws of physics, be it Newton’s laws or the Schrödinger equation, are condensed, abstract representations of these latent principles. As in Newton’s case, realizing that a falling apple follows the same laws as the orbits of the planets means understanding that the world is much more ordered and less random than it appears.
Generative Models
“What I cannot create, I do not understand.” Richard Feynman
The goal of a generative model is to learn an efficient representation of the latent structure behind some input data x (such as training on a lot of pictures of faces our sound files), to understand which laws govern its distribution, and to use this to generate new outputs x’ which shares key features of the input data x.
The fact that your input data is not truly random means that there is a structure behind x, which means that there are certain non-trivial (trivial would just be the random dots) probability distributions responsible for generating the data. But these probability distributions are usually extremely complex for high-dimensional input and generally hard to parse out.
This is where deep learning comes to the rescue, which has proven again and again to be very successful at capturing all kinds of complicated, non-linear correlations within data, and allowing us to make good use of them.
Generative models can take many shapes and forms, but variational autoencoders are, I believe, a very instructive example, so we’ll take a closer look at how they work now.
Latent Variables
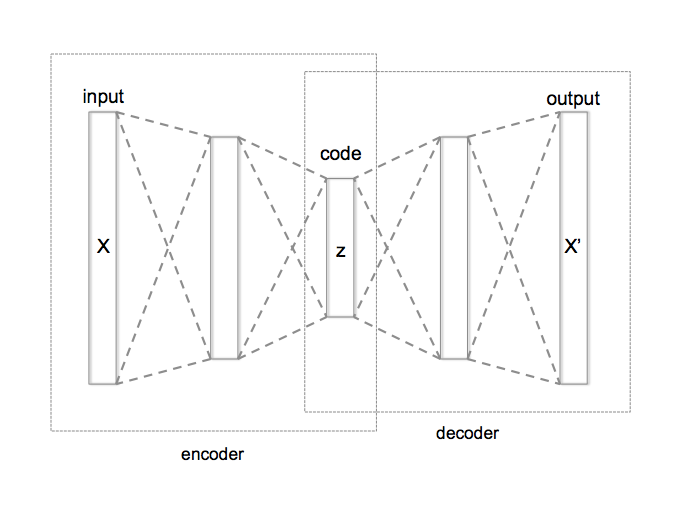
A Variational Autoencoder is usually constructed using two deep neural networks.
The first deep neural network learns a latent (usually lower-dimensional) representation of the input data x.
It encodes this latent structure in probability distributions over some latent variables, which we denote by z. The main task then is to find what is called the posterior over the latent variables given our data, written as p(z|x) in the language of probability theory. This step is, accordingly, called the encoder.
Note that this is somewhat similar to what a discriminative neural network is doing in supervised classification tasks: it is trained to find structure in data that is connected to the labels, allowing it, for example, to distinguish between pictures of cats vs. dogs.
Only that in the case of generative models, we are looking for probability distributions of the data itself, which, for the autoencoder, we encode in those of the latent variables.
For the more technically interested: one way to achieve this is by introducing a class of approximate prior distribution over the latent variables (e.g. a combination of Gaussians) and training the network to find the parameters of these distributions (e.g. the means and covariances) that are as close as possible to the real prior (measured by the KL divergence, for instance).
Once the model has learned the probability distribution over the latent variables z, it can use this knowledge to generate new data x’ by sampling from p(z|x) and doing the reverse task of the first network, which means looking for the posterior of the data conditioned on the latent variables, given by p(x’|z).
In other words: how would new data look like given the distribution of latent variables p(z|x) that we have learned earlier by using the first network?
This step is then called the decoder or generative model.
We can construct it by likewise training a neural network to map the random variables z onto new data x’.
To sum up what a variational autoencoder is doing:
- Learn the posterior x → z from the input data: p(z|x)
- Generate new data z →x’ from the model: p(x’|z)
Do Helmholtz machines dream of electric sheep?
“The electric things have their life too. Paltry as those lives are.” Philip K. Dick, Do Androids Dream of Electric Sheep
There is one key ingredient missing: how do we train generative models?
This can be quite tricky. Training them is usually much harder than training discriminative models. Because you really really need to understand something before you can create it yourself: recognizing a Beethoven symphony is easier than composing one yourself.
To train the model, we need some loss function to train on, and an algorithm to implement it, while multiple networks need to be trained at the same time.
One of the earliest generative models is called Helmholtz Machines, developed in 1995 by Dayan, Hinton, and Neal.
Helmholtz Machines can be trained using the so-called Wake-sleep algorithm.
In the wake phase, the network looks at data x from the world and tries to infer the posterior of the latent states p(z|x).
In the sleep phase, the network generates (“dreams”) new data from p(x’|z) based on its internal model of the world, and tries to make its dreams converge with reality.
In both steps, the machine is trained to minimize the free energy (also called “surprise”) of the model. By progressively minimizing the surprise (which can then be incorporated through methods like gradient descent), generated data and real data become more and more alike.
Different Generative Models
There are several types of generative models used in modern deep learning, which built on Helmholtz machines but overcome some of their problems (such as the Wake-Sleep algorithm being inefficient/not converging).
In the Variational Autoencoder introduced above, the aim is to reconstruct the input data as well as possible. This can be useful for practical applications, such as data denoising or reconstructing missing parts of your data. It is trained by minimizing something called the ELBO (Evidence Lower Bound).
Another powerful approach is given by General Adversarial Nets (GAN), which were used to generate the faces you saw earlier.
In GANs, a discriminator network is introduced on top of a generative model, which is then trained to distinguish if its input is real data x or generated data x’. No encoder network is used, but z’s are sampled at random and the generative model is trained to make it as hard as possible for the discriminator network to tell if the output data is real and fake.
Note that the ideas behind generative models are very abstract and, therefore, very flexible. You can train them on all kinds of data (not only pictures) such as Recurrent Neural Networks (RNNs) on time series data, e.g. fMRI data or spike trains from the brain. After inferring the latent structure behind the data, the trained models can be analyzed to improve understanding of underlying processes in the brain (e.g. dynamical systems properties connected to mental illness, etc.).
Generative Models and Cognition
It’s already really impressive what generative models can achieve, but they can also bring us a step further in understanding how our brains work. They do not only passively classify the world, but actively capture essential structures within it and incorporate those into the model itself. Just as we all live in our own inner worlds created by our brains, generative models create tiny inner worlds of their own.
As proponents of The Bayesian Brain Hypothesis argue, this is a key feature of our cognitive apparatus. Our brain constantly builds latent internal representations that in some way reflect the probability distributions of the real world, but also simplify them and focus on what is most important (because the world is far too complex to be simulated in its entirety by your brain).
In the spirit of generative models, once you can create something you know how it works. And so building machines that can dream and imagine might take us a long way towards understanding how we dream and imagine ourselves.
About the AuthorManuel Brenner studied Physics at the University of Heidelberg and is now pursuing his PhD in Theoretical Neuroscience at the Central Institute for Mental Health in Mannheim at the intersection between AI, Neuroscience and Mental Health. He is head of Content Creation for ACIT, for which he hosts the ACIT Science Podcast. He is interested in music, photography, chess, meditation, cooking, and many other things. Connect with him on LinkedIn at https://www.linkedin.com/in/manuel-brenner-772261191/