How our brain evolved to look into the future
If you can look into the seeds of time, and say which grain will grow and which will not…
Macbeth, William Shakespeare
Life is riddled with uncertainty, and no one can tell the future. According to Blaise Pascal, we sail within a vast sphere, ever drifting in uncertainty, driven from end to end. No one knows when death might come, when life will throw hardships at us, when life will reward us.
While we all have to learn this dreary lesson at some point in our lives, we nevertheless manage admiringly well to prevail in a universe shaped by uncertainty. We build houses, we put money into our bank account, we save up for our retirement fund and for our grandchildren. We shape stable relationships and build monuments to last lifetimes. We have a sense of control about what’s going on and we deserve to have it.
This is pretty remarkable for something such as us, who came to exist out of the random and chaotic fancies of evolution. How did we develop the ability to carve a sense of certainty out of a future defined by uncertainty?
The Bayesian brain hypothesis argues that there is a deep hidden structure behind our behavior, the roots of which reach far back into the very nature of life. It states that in a way, brains do little else than predicting a future and enforcing this desired future, that brains, in unison with the laws of living systems, always fight an uphill battle against the surprises nature has in store for them.

The Homeostatic Imperative
Homeostasis is the underlying principle behind all life. It derives from the Latin homeo (equal) and stasis (to stand still) and was coined in 1926 by Walter Bradford Cannon. Homeostasis symbolizes the maintenance of physical and chemical processes within living systems that keep living systems whole and stop them from dissipating away (I went into more detail on this in my article on the origins of life). It is the principle of self-organization withstanding nature’s tendency to disorder.
In his book The Strange Order of Things, Antonio Damasio argues that the term is misleading, as homeostasis signifies much more than just a standstill. Life is a self-realizing principle that is not just satisfied with maintaining its function in the present. If you take two competing organisms, where one is complacent with life as it is, while there is another one optimized to fare well for ages to come, which one will have a larger chance for surviving for millions and billions of years? Life as we find it in today’s world always implicitly aims at propelling itself far into the future, because in the past it evolved traits that would incentivize it to continue propelling itself onwards into the future.
To keep the wheel rolling, to keep breathing and pushing forward.

Predicting the Future
People have always tried predicting and changing the future. In ancient times, fortune-telling was a sophisticated craft reserved for priests and shamans. The most famous example of this might be the Oracle of Delphi, consulted for hundreds of years by Greek statesmen and Roman emperors alike. Ancient politics was a time of much uncertainty, and we shouldn’t be too judgy about people’s desire to see it reduced.
But from a more modern scientific perspective, we have come to realize that it is unlikely that inhaling poisonous fumes and talking in riddles while in a state of trance will give us any real insights into the workings of the world. In order to reduce uncertainty about the future, we (and our brains with it) need to take a more pedestrian approach, trying to predict it as well as possible based on what we already know about the world. What can I expect to happen tomorrow based on what I observe in the world today, and in what sense should I direct my action in order to get the results most advantageous for my survival?
Bayes‘ Theorem
Unpublished during his lifetime, 18th century reverent Thomas Bayes came up with a neat little theorem that would later turn out to be tremendously useful in many areas. It’s really quite simple, but that doesn’t keep it from bringing Bayes’name the honor of adorning one of the hottest theories in modern cognitive science.
Here we can see a blue, glowing version of it:
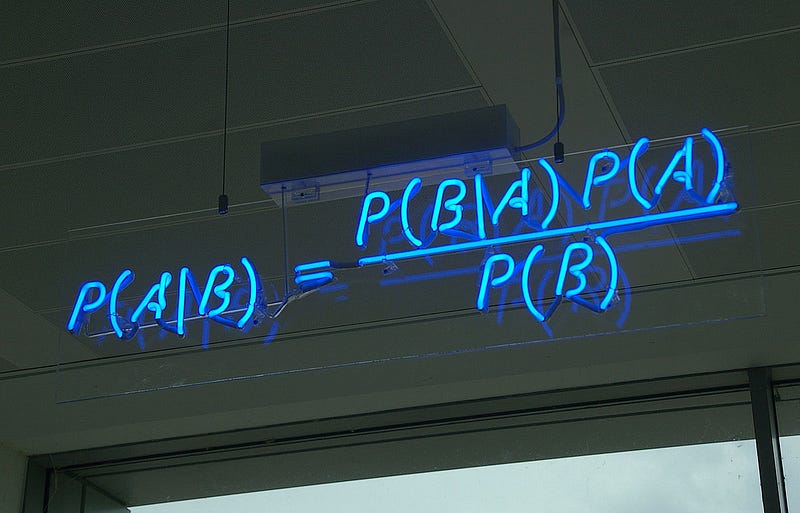
Bayes’ theorem states that the probability of A given B is the same as the probability of B given A times the probability of A, divided by the probability of B.
It gives us the probability for certain things to happen when we already know the probabilities of other, related things happening.
You can hopefully already guess why this might come in handy when trying to predict the future.
A popular example for applying Bayes’ theorem takes a look at the weather, eternal source of uncertainty and frustration about the cruelty of nature.

Let’s say you went for a walk but for some reason got lost in the arid and endless expanses of a desert. You were planning to take a stroll through the park so you only brought a small bottle of water to drink. After being lost for three days you are naturally quite thirsty. You scan the sky for a cloud in the morning, and lo and behold, there at the horizon you see a small one.
What is the probability for it to rain, and for you to be saved from dying of dehydration?
We are looking for the probability P(Rain|Cloud), so for the conditional probability for it to rain given you observe a cloud. We need:
- P(Cloud|Rain): if it rains on a given day, does the day start off with a cloud in the sky? Let’s say 80% of all rainy days in the desert started off cloudy. This means that it is highly likely that there was a cloud to begin with in case it rained that day.
- P(Cloud): the chance for there to be a cloud at all in the desert on a given day is pretty small: it is at 10%.
- P(Rain): the odds of it raining are even smaller. It only rains on every hundredth day in the desert, so the probability is at 1%.
The total probability for rain given that you observe a cloud is then given by:
P(Rain|Cloud)=P(Cloud|Rain)*P(Rain)/P(Cloud)=0.8*0.01/0.10=0.08
After seeing the cloud, you can say that with around 8 percent probability it is going to rain. A small consolation, but better than nothing.
It is crucial to note that all three other probabilities are essential when calculating the conditional probability you are interested in. Discarding one can significantly alter the result you are looking for.
False Positives
Bayes’ theorem helps us correct for false positives, e.g. when we assume that an event is informative about a result that would in itself be really unlikely. A famous example of this is cancer tests (or for any other rare disease).
Say only 0.1% of the population has a certain type of cancer. Your doctor tells you about a new, improved cancer test that detects cancer in 90% of the cases given the patient really has cancer. The downside is that it also detects cancer in approximately 9% of the measurements when cancer is not really there.
You are a naturally anxious person so you want to relieve your anxiety by taking the test. You have a positive result. You are really scared for a second because after all, the odds of you having cancer are at 90%, aren’t they?
No, because you can quickly apply Bayes’ theorem to figure out the real odds of you having cancer. Note that in this case, you need to divide out both the probability for having a real positive and the odds of having a false positive:
P(cancer|positive result)=P(positive result|cancer)*p(cancer)/(p(positive result)*p(cancer)+p(false positive)*p(not having cancer))= 9.17%
So again you shouldn’t be too concerned (which will be difficult considering you took the test out of anxiety to begin with), because having cancer is so unlikely that the chance of getting a false positive is about ten times higher than getting a positive result and actually having cancer.
A Note on Unicorns

It is therefore helpful for anyone interested in predicting the future to have a good idea of the prior probabilities for events to happen.
In order to judge how informative one event (e.g. the seeing of a cloud or a positive cancer test) is for predicting another (for it to rain or for you to have cancer), we need to have representations of the overall probabilities for rain or cancer when we are observing clouds or cancer tests.
As the brain constantly judges probabilities when classifying the information that the senses gather about the external world, you can probably start to guess why there could be something Bayesian to the way it operates.
Say you see the blurry outline of an animal with four legs galloping along the horizon. It looks like there is a long and pointy object attached to the animal’s forehead.
Does your brain automatically jump to the conclusion that it’s a unicorn?
If you are not insane, probably not, because the probability of observing a unicorn given the shape you are observing P(unicorn|shape) has to be weighted by the fact that the prior probability of observing a unicorn, P(unicorn), is very likely 0 within in our universe.
Internal models of the world
If the brain wants to model the behavior of the world, especially that of the future, the brain needs to have an internal model of what the world is like in order to understand what the world might become.
The brain needs to be able to update this internal model of the world after receiving new information about the state of the world, e.g. by receiving new samples. Say that you regularly see a unicorn on your daily commute to work. How long will it take you to start wondering if your assumption that there are no unicorns is still true? Or say 20 out of 50 people that get positive cancer tests actually turn out to have cancer. How confident do you remain about the estimate that only 9.17% of all positive results should mean that the patient actually has cancer?
Updating the probability distribution of the internal model based on new information in a statistically optimal way is called Bayesian Inference.
We routinely observe the brain doing this kind of inference in behavioral experiments, or when relating sensory inputs to each other: it has been shown that in Pavlovian associated stimulus experiments mutual information between different stimuli is optimally accounted for (see p.16 here for an overview). Another great example is the famous 1992 visual motion study by Britten et. al, showing that monkey brains manage to approach Bayes optimal decoding rates when trying to decode the coherence of a visual motion based on the neural responses/firing rates to the stimulus.
It turns out that the brain predicts in predictable ways.
The Bayesian Brain Hypothesis
Now we are prepared to look deeper into what the Bayesian Brain hypothesis actually entails.
The Bayesian brain exists in an external world and is endowed with an internal representation of this external world. The two are separated from each other by what is called a Markov blanket.
The brain is trying to infer the causes of its sensations based on generative models of the world. In order to successfully model the external world, it must be in some way capable of simulating what is going on in the outside world. In the words of Karl Friston (taken from here):
If the brain is making inferences about the causes of its sensations then it
must have a model of the causal relationships (connections) among
(hidden) states of the world that cause sensory input. It follows that
neuronal connections encode (model) causal connections that conspire
to produce sensory information.
This is the first crucial point in understanding the Bayesian brain hypothesis. It is a profound point: the internal model of the world within the brain suggests that processes in the brain model processes in the physical world. In order to successfully predict the future, the brain needs to run simulations of the world on its own hardware. These processes need to follow a causality similar to that of the external world, and a world of its own comes alive in the brain observing it.
The second point refers back to Bayesian Inference: it entails that the brain is optimal/optimized in some sense, as we should come to expect when nature is concerned.
As I pointed out earlier, when classifying the content of perceptions and making decisions under uncertainty, the Bayesian brain works at an approximately Bayes optimal level, meaning that it takes into account all available information and all probabilistic constraints as well as it possibly can when inferring future (hidden) states of the world.
There are several names you can give to the quantity that is optimized, but as often the case with deep and unifying theories, it turns out that different perspectives optimize different things that end up being the same quantity. One way of looking at it is as evidence, which in information theory is equal to maximizing the mutual information between sense-data and the internal model of the world.
Free Energy
In my article on The Thermodynamics of Free Will, I looked in more detail at Karl Friston’s theory of Active Inference (roughly speaking the theory of what Bayesian brains do).
Free energy is minimized to optimize the evidence or marginal likelihood of a model, which Friston identifies with minimizing something called the surprise of the model (so minimizing experiencing something that does not fit into your model of the world).
The theory further incorporates an active component into the behavior of living systems such as brains, which allows the system to perform actions in the world. You cannot only dream up the future, but you can actively change the future by acting on the world and making your expectations come true.
It’s no coincidence that Active Inference is abbreviated by AI, as Karl Friston here, and he believes that “within five to 10 years, most machine learning would incorporate free energy minimization”.
This brings us back to Damasio’s critique of homeostasis:
Living systems are not static, but they act in the world in order to minimize surprise and persist in a future shaped by uncertainty.
The minimized free energy relates to entropy because the time-average over the surprise gives us a measure of the entropy. This has profound physical consequences, because as Friston states:
This means that a Bayesian brain that tries to maximize its
evidence is implicitly trying to minimize its entropy. In other words, it
resists the second law of thermodynamics and provides a principled
explanation for self organization in the face of a natural tendency to
disorder.
The Bayesian brain hypothesis is, therefore, a theory of fundamental scope. It ties up the behavior of the brain with the homeostatic imperative, with life’s struggle to survive in a world that would much rather dissipate.
How do we observe the Bayesian brain?
To propose a theory of grand scope is one thing. To find evidence for it in the way the brain behaves is another. If the brain behaves as a Bayesian brain, we need to further our understanding of how the brain actually implements Bayesian Inference.
Bayesian Inference is thought to take place on a great many layers of cognition, from motor control to attention and working memory. Every cognitive task brings with it its own predictions, own internal models, and unique timescales.
One of the promising attempts of realizing it is called Predictive Coding, which does just what the Bayesian brain is supposed to do: its algorithms prepare for the future by changing the parameters of their predictions in a way as to minimize surprise in case they are confronted with the same situation again. Evidence for this has e.g. been found in word prediction experiments with the so-called N400 effect (see here or here)
Cognitive Science is realizing that the brain is not just a detector that passively takes in information about the world and reacts to it. It constantly shapes its vision of the world by making assumptions about how the world is and how the world will be, doing so in a top-down manner (meaning that higher-order concepts shape the way lower-order sensory data is perceived in the first place, as described in the unicorn example). This has caused researchers to adopt the wonderful concept of reality as controlled hallucination (see Anil Seth’s Ted Talk for more), exemplified by probands hallucinating hearing the word “kick” instead of “pick” after having read “kick” beforehand, as shown in this study.
Hallucinating reality in a predictable way gives us a decisive evolutionary advantage, one that we direly need when hoping to find structure in a tumultuous and complicated world.
Scientists are still passionately fighting over the validity of the theory and over the big question of how the brain actually manages to incorporate Bayesian Inference on a functional level. Further research is warranted before we make any definitive claims. But I think the beauty of the theory and the evidence we have seen thus far can make us hopeful that we are on a good track.
That we are getting closer to cracking the secrets of the most mysterious object in the universe, the object which allows us to observe the world and navigate within it, which makes us live and die and hope for a better future (and you probably already have an internal representation of how I will end this sentence): our very own Bayesian brain.
by Manuel Brenner