…how the brain creates conceptual spaces

We think every day, but it’s hard to pinpoint what exactly we mean by the word. When we try to understand thought, we have to grasp thought by thinking about thought itself, which feels ever so slightly elusive and circular.
And then there are a hundred different ways of thinking about a thing. What do you actually do when thinking about an apple? When thinking of the color red? When thinking about abstract concepts like love, grief, pride, existence?
Wikipedia defines thought as an “aim-oriented flow of ideas and associations that can lead to a reality-oriented conclusion”.
The flow of ideas is easily observable. Think of an apple, and see what happens, which different perceptual dimensions present themselves. A glimpse of red-green peel, a hard-to-define sweet and fruity taste, maybe a hint of sourness, the crunchy sound of a bite, the sensation of juice running down your hand.
The reality-oriented conclusion is naturally given: we shouldn’t forget that our thinking has evolved to serve an evolutionary purpose. Thought exists because it helps the genetic machinery at the heart of life propel itself onward into the future. Thought exists because it allows us to observe useful, structured patterns in the messy world in which we find ourselves. To separate the wheat of useful information from the chaff of irrelevant one.
It serves a purpose to know an apple from a poisonous fruit, to understand if it’s ripe and ready to be eaten, to understand what an apple is, what properties it has although every individual apple you will encounter is ever so slightly different.
It serves a purpose to be able to compare apples and oranges. And it makes sense to be able to communicate your thoughts with the people surrounding you, to tell them what it is you feel, what it is you saw.
There are certain tasks that we constantly need in everyday life, so the brain is optimized to do the job. On the other hand, we are not good at doing “thinking” that computers are really good at (questions like what is 159476 times 6042034869?). Solving calculations like 159476 times 6042034869 aren’t the most relevant tasks we need to be able to solve when sprinting away from a tiger.
Hearing something can change your outlook onto the world, can teach you new ways of thinking, new concepts in which to express patterns in the world. This can have value for the whole society you live in. Being able to explain something to someone else means that fewer people have to figure stuff out anew each time.
Think of science: private knowledge becomes communal knowledge.
Therefore, people within a community need to agree on a common conceptual framework that they can effectively teach to their descendants and adjust quickly as a whole society.
Patterns in Thought
To give a preliminary summary and working definition of (at least a very relevant subsection) of “thought”, we have
- Classification of patterns in the external world defined by…
- …fluid and quickly learnable concepts (this is an apple vs. this is a peach)
- …allowing for comparisons between objects along many different abstract dimensions (this apple is larger, sweeter, redder, rounder, etc.)
- …metacognition: having an abstract understanding of the conceptual framework itself and being able to reason within that framework
Linking them to their evolutionary function helps us understand why they exist and which tasks they are optimized to do. After all, evolution did not bring forth thinking only to entertain us.
And speaking about evolution: can we find “evolutionary ancestors” of thinking in other, possibly more primitive cognitive functions?
Might thinking have evolved out an infrastructure already in place to serve a different purpose?
Architecture and Functionality
Operations in the brain are closely related to the content of our phenomenal world, the world of our conscious experience. When there is an auditory stimulus, we see activity in certain brain regions correlated with the conscious experience of noise. When we see something, we can trace signals moving from the retina to the occipital lobe, home of the visual cortex. The way thought is implemented in the brain, therefore, should coincide with the function and phenomenality of the thought.
It is often emphasized that computers work very differently from brains, which is reflected in the way they are built. Computers to this day are still based on the von Neumann architecture. All computations are carried out on 1s and 0s. Inputs into the computer are transformed into 1s and 0s, which are then manipulated in specific ways to carry output computations. The output is similarily given by 1s and 0s, which are then translated back into output comprehensible to the user. The von Neumann architecture is in principle based on that of a Turing machine, which manipulates information on the symbolic level (for more detail, see here for my non-technical guide to Turing machines).
Research in AI is concerned with building machines that “think”. Machines have gotten much better at learning patterns from data, at extracting useful information and relevant feature from very high-dimensional data sets.
But computers don’t learn abstract concepts to apply to the world as easily. They usually can’t understand what an apple is after seeing just one exemplar. They can’t as easily connect different conceptual layers with each other, and make comparisons between different concepts. They can’t reason or adjust their behavior flexibly when new challenges are faced.
In my article on Ants and the Problems with Neural Networks, I looked in more depth at the relationship between the functionality of cognitive processes and their most efficient (conjectured) computational implementation. It makes sense to assume that the shape and form of thought should in some way reflect the way it is implemented. Nature is parsimonious in spending its resources and generally picks out the most efficient architecture to do the job.
Conceptual Spaces
In the rest of this article, I will focus on the idea of a conceptual space introduced by Peter Gardenfors in his (very appropriately titled) book Conceptual Spaces (2000) (also see this talk for some details I can’t cover here).
If you’ve read something about machine learning you might be familiar with the concept of a feature space. The data you are feeding into the networks is represented in feature spaces. You feed pixels characterized by color information into a network and let it, for example, do its work figuring out what’s in the picture based on the sensory input (a cat, a dog, etc.) It’s something like that with information coming in through our senses that is processed by our brain.
A conceptual space now is defined as the entity spanned by several quality dimensions, in which multimodal (more than one type of data, like visual and auditory combined) concepts are represented. These features can cover an immense range of things, like size, color, pitch, tone, length, light/darkness, temperature, space itself, taste, shape, sweetness, sourness, etc.
A concept is then a topological region in conceptual space. You can think of them as multi-dimensional generalizations of properties like the color red, which are simply one-dimensional features.
Topological means that the regions the spaces are partitioned in are fully connected and fulfill certain geometric properties, namely that they are convex. This means that if a point z lies in between a point x and y and both belong to the same concept, then that point has to lie in that concept as well.
One way of implementing this is by so-called Voronoi tesselations, here displayed for a two-dimensional space:

These tesselations carve up the space in convex regions radiating from the black dots. You can think of them as primitive versions of concepts in two-dimensional quality spaces.
According to Gardenfors, these convex tesselations allow for efficient communication, because they get rid of any ambiguity between different subconcepts (the spaces around the prototypes are clearly shaped out and don’t have any holes in them, which would cause confusion if you compare different elements of the space and try to gauge how similar they are).
Say one dimension is how voiced a sound you are making is and the other dimension determines at which place in your mouth the sound is produced. The tesselations then correspond to the concepts of letters deduced from the sound you are hearing and mapped onto the position of the tongue and the degree of voicing in the person you are listening to.
This allows you to classify the consonants b and p, m and n, d and t, etc., depending on the position of your tongue in your mouth and on how hard you push. Notice that extracting this information is crucial for voice recognition software like speech-to-text or Apple’s Siri and Amazon’s Alexa, and of course, in our case, for understanding other people.
The tesselations have points at the center, which can be thought of as the prototypes of a given concept. There is a way of saying “d” that makes it unambiguously clear that you are really saying “d”, while with people that mumble or are speaking a foreign language it’s sometimes harder to properly map the sounds you are hearing onto syllables and words.
High dimensional conceptual spaces
The ability to learn concepts shows that the metric of concept spaces exerts some flexibility. It can be changed, for instance, when we learn that certain subdimensions are more important for classification than others, causing the weight structure of the different feature subdimensions to adapt.
Think of practicing something: we can zoom into a space and make its subdivisions smaller and smaller. Professional sommeliers can perceive the taste of wines with much more granularity than the layman, and professional musicians can pick out chords and instruments in an orchestral piece with ease.
Children famously (and sometimes hilariously) overgeneralize concepts from single examples, but at the same time, this can be advantageous because they don’t need to see many examples before they can learn something. Concepts then get more and more sophisticated as time moves on and more examples are seen.
Concept learning is incremental. There is a hierarchy to the way we learn concepts: we can stack up more and more abstract concepts (likes the rules of the society you live in) composed out of more and more features and patterns on top of each other and flesh out more and more fine-grained distinctions between them when we become adults.
Conceptual spaces can be extended to very large dimensions: we’ve covered the example of an apple, but learning of high-dimensional conceptual spaces can also lead to problematic over-generalizations, as embodied by racial stereotyping.
The idea of race that has shaped so many conflicts of modernity can be thought of in terms of Voronoi tesselations: the Nazi ideology taught the supremacy of the Aryan superhuman (blond, blue-eyed and able-bodied, the archetype at the center of the space representing the concept of the Aryan race). Everyone similar enough to that being was part of the ingroup, while everyone that differed along significant traits was not, and deemed inferior. While it turned out that the traits defining these concepts were arbitrary and not at all grounded in any biological facts, they were still spread by fervent ideologues, and readily learned by brains all over the country.
Symbolic vs. subsymbolic knowledge
These things aside, let’s return to the question of the relationship between the geometry of thought and its potential implementations in the hardware of the brain.
Conceptual spaces aim at bridging the chasm between symbolic and subsymbolic theories of knowledge representation in the brain.
Pure symbolic thinking is bad at concept formation: the symbols themselves don’t necessarily need to mean a lot, and similarity measures do not transport well from the symbolic level to the semantic level. When you compare the words “nap”, “gap”, “rap” or the numbers 100000 and 000001 in binary, they are all not that far apart symbolically but are not necessarily very close in meaning to each other. In the case of the symbolic language of our genetic code, the DNA sequence coding for a protein is quite arbitrary, and doesn’t have any functional underpinning (as I discuss in more detail here).
So if the brain works by manipulating symbolic representations of information, it would be hardpressed to process similarities between its content, while a pure subsymbolic representation would make it hard to fluidly learn new concepts (this problem is frequently encountered in machine learning applications: after some small changes to the input, the network becomes completely useless at classifying it and has to learn everything anew).
Similarity and metrics in feature space
Conceptual spaces avoid some of these problems because they are modeled as metric spaces (spaces that have a measure of distance).
They effectively encode similarity relations between entities within the spaces. We can easily and intuitively answer questions like: Which of these five apples look most similar to each other? How much does your friend look like Brad Pitt? How similar to each other are New York and Tel Aviv? Does this word sound a bit like this other word?
Answers to these questions cannot be hardwired as look-up-tables into our brains: there is an infinite amount of possible relations/comparisons that you could think of, so the brain needs to be able to compute answers on the fly.
Spatial representations and the genesis of thought
All life forms that we know find themselves living in a three-dimensional space (ignoring string theory for a moment), and living in this three-dimensional space has had its influence on our evolutionary trajectories.
In her book Mind in Motion, Barbara Tversky proposes nine laws of cognition. According to her sixth law, spatial thinking is the foundation of abstract thought.
The underlying hypothesis is that we first evolved the ability to navigate successfully in three-dimensional space, figuring out where we were, where our bodies were, how to move them, etc., and slowly came to recycle already present brain regions that were first used for tasks like moving in space to achieve new ways of thinking.
I can’t get into this hypothesis in much detail, but I’m mentioning it here because the geometrical properties of conceptual spaces can help understand it a lot better, and the neurobiological foundation of conceptual spaces brings some convincing evidence for it to the table.
Spatial representations within the brain
Spatial representations in the brain are incorporated in its functional architecture. The 2014 Nobel prize in medicine was awarded to O’Keefe and Dostrovsky for their discovery of place-cells in 1971, combined with the discovery of grid cells in 2005 by Edvard and May-Britt Moser.
The firing of these cells is connected to the spatial position of animals, such as rats or human beings, and they are believed to serve as a cognitive map of places (see this animation for an illustration). These cells are mostly found in the hippocampus and the entorhinal cortex, which are responsible for memory, navigation, and perception of time.
The firing of a place cell represents the position of the animal in physical space, and this position is reflected by the interconnections of the place cell or grid cells to neighboring cells.
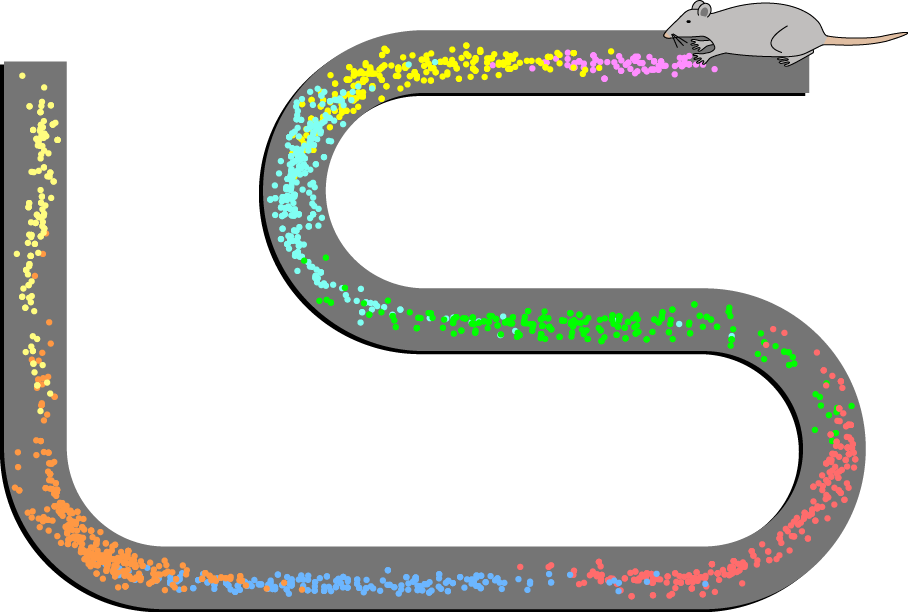
Their patterns of excitation can represent an abstract vector space, not only three-dimensional space, so their firing patterns can in principle encode all kinds of spatial information (distances and locations in spaces). Therefore, these structures could also be used to encode very different kinds of metric spaces.
It looks like mother nature made good use of this.
New studies indicate that abstract conceptual spaces are mapped by using the same infrastructure of place- and grid cells in the entorhinal cortex and hippocampus (for more detail, see here, here, here or here) that maps spatial locations and orientation.
Thus the notion of a cognitive space is not only metaphorical, because implementing them with place-and grid cells allows the brain to encode locations in abstract conceptual spaces and compute measures within those spaces efficiently.
As I pointed out in the beginning, this supports the notion that we should find evidence for a tight relationship between the functionality of cognitive processes (like thoughts) and the structure of their computational and biological implementation within the brain.
It looks like abstract thought, at least to some extent, truly evolved out of spatial thinking.
Teaching machines the geometry of thought
It has to be noted that these theories are still new and in the process of being fully fleshed out, but I think research is pointing in exciting directions. Understanding thought and its origins in spatial perception can bring us many new insights into higher cognitive functions of the brain.
And it might likewise give new impulses on how to build intelligent systems that exert more “human-like” traits in the way they process information and learn new things.
If we, for instance, could combine deep neural networks working on pattern recognition and information extraction from (multimodal) input data with architectures, inspired by place- and grid cells, that allowed efficient mapping of similarities between patterns extracted from inputs and less data-heavy learning of higher-order concepts, we might teach machines the geometry of our own thought, and so teach them to become more and more like us.
About the AuthorManuel Brenner studied Physics at the University of Heidelberg and is now pursuing his PhD in Theoretical Neuroscience at the Central Institute for Mental Health in Mannheim at the intersection between AI, Neuroscience and Mental Health. He is head of Content Creation for ACIT, for which he hosts the ACIT Science Podcast. He is interested in music, photography, chess, meditation, cooking, and many other things. Connect with him on LinkedIn at https://www.linkedin.com/in/manuel-brenner-772261191/